Chapitre 3- Statistiques - effectifs et fréquences
- Trier des données en un tableau valeurs/effectifs ou classes/effectifs.
- Calculer une fréquence à partir d'un effectif et de l'effectif total.
- Retrouver un effectif à partir d'une fréquence et de l'effectif total.
- Passer de l'écriture décimale au pourcentage.
- Représenter une série statistique à l'aide d'un diagramme
- Exploiter les données d'un diagramme
IIntroduction
1Généralités
Nous raisonnerons sur le même exemple donné ci-après.
Dans une étude statistique, on choisit une population dont on étudit le caractère prenant des valeurs numériques différentes selon l\individu. L'ensemble des valeurs forme une série statistique.
On choisit une population de 12 élèves qui ont participé à un contrôle dont voici les notes : $$ \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|} \hline 9 & 10 & 6 & 16 & 7 & 11 & 11 & 2 & 14 & 11 & 6 & 14 \\ \hline \end{array} $$
- Le caractère étudié est "la note du contrôle"
- Les notes prennent différentes valeurs entre 2 et 16
L'étendue de la série statistique est la différence entre la plus petite et la plus grande note. Ici, l'étendue vaut 16-2=14.
2Tableaux d'effectifs et de fréquences
Pour mieux représenter la série statistique, on doit trier le tableau, et l'organiser par rapport aux effectifs ou aux fréquences :
- L'effectif total est le nombre d'individus de la population
- L'effectif d'une valeur est le nombre d'individus dont le caractère à cette valeur
- La fréquence d'une valeur est le quotient \(\frac{\text{effectif de la valeur}}{\text{effectif total}}\)
Une fréquence est toujours plus petite que 1. La fréquence 1 représente "tous les individus", tandis que la fréquence 0 représente "aucun individu".
La fréquence de la note 11 vaut donc \(\frac{3}{12} = \frac{1}{4} = 0.25\).
Connaissant la fréquence d'une valeur et l'effectif total, on peut retrouver l'effectif de la valeur par la formule : $$ \text{effectif de la valeur} = \text{fréquence de la valeur} \times \text{effectif total} $$
La fréquence de la note 11 valant 0.25 et l'effectif total valant 12, on retrouve bien l'effectif \(3 = 0.25 \times 12\).
Le pourcentage d'une valeur s'obtient en multipliant la fréquence par 100.
Le pourcentage de notes valant 11 est de \(0.25 \times 100 = 25\%\)
Atableau d'effectifs
On peut représenter la série à l'aide d'un tableau d'effectifs :
- C'est un tableau de deux lignes à simple entrée
- La première ligne correspond aux valeurs triées par ordre croissant
- La deuxième ligne correspond aux effectifs des valeurs
Sur notre exemple : $$ \begin{array}{|l|c|c|c|c|c|c|c|c|} \hline \text{Notes} & 2 & 6 & 7 & 9 & 10 & 11 & 14 & 16 \\ \hline \text{Effectifs} & 1 & 2 & 1 & 1 & 1 & 3 & 2 & 1 \\ \hline \end{array} $$ En lisant la 6-ème colonne, on retrouve l'information suivante : "la note 11 apparaît 3 fois".
Attention, le nombre de valeurs apparaissant dans le tableau n'est plus 12. Pour retrouver l'effectif total, il faut additionner tous les effectifs de la deuxième ligne: \(1 + 2 + 1 + 1 + 1 + 3 + 2 + 1 = 12\)
Btableau de fréquences
On peut représenter la série à l'aide d'un tableau de fréquences :
- C'est un tableau de deux lignes à simple entrée
- La première ligne correspond aux valeurs triées par ordre croissant
- La deuxième ligne correspond aux fréquences des valeurs
Sur notre exemple : $$ \begin{array}{|l|c|c|c|c|c|c|c|c|} \hline \text{Notes} & 2 & 6 & 7 & 9 & 10 & 11 & 14 & 16 \\ \hline \text{Fréquences} & \frac{1}{12}\simeq 0.08 & \frac{1}{6}\simeq 0.17 & \frac{1}{12}\simeq 0.08 & \frac{1}{12}\simeq 0.08 &\frac{1}{12}\simeq 0.08 & \frac{1}{4}=0.25 & \frac{1}{6}\simeq 0.17 & \frac{1}{12}\simeq 0.08 \\ \hline \end{array} $$ En lisant la 6-ème colonne, on retrouve l'information suivante : "Un quart des élèves ont eu la note 11".
On arrondit généralement à 2 chiffres après la virgule.
3Données regroupées en classes
Il est possible que les valeurs d'une série statistique soient regroupées par classes de mêmes amplitudes :
Sur notre exemple, on regroupe les notes en 4 classes :
- Les notes allant de 0 à 5 (non compris), représentées par l'intervalle \([0;5[\)
- Les notes allant de 5 à 10 (non compris), représentées par l'intervalle \([5;10[\)
- Les notes allant de 10 à 15 (non compris), représentées par l'intervalle \([10;15[\)
- Les notes allant de 15 à 20 (non compris), représentées par l'intervalle \([15;20[\)
Les classes sont souvent utilisées pour un nombre important de valeurs présentant des nombres décimaux.
On peut alors construire les 4 tableaux (effectifs, fréquences, ECC, FCC) non pas sur les valeurs des notes, mais sur ces 4 classes :
ATableau d'effectifs
Pour obtenir l'effectif de la classe \([5;10[\), il fautr additionner les effectifs des valeurs \(6\), \(7\) et \(9\) :
$$ \begin{array}{|l|c|c|c|c|} \hline \text{Notes} & [0;5[ & [5;10[ & [10;15[ & [15;20[ \\ \hline \text{Effectifs} & 1 & 4 & 6 & 1 \\ \hline \end{array}
$$
On retrouve bien 12 comme effectif total en additionnant les valeurs de la deuxième ligne.
BTableau de fréquences
$$ \begin{array}{|l|c|c|c|c|} \hline \text{Notes} & [0;5[ & [5;10[ & [10;15[ & [15;20[ \\ \hline \text{Fréquences} & \frac{1}{12}\simeq 0.08 & \frac{4}{12}\simeq 0.33 & \frac{6}{12}=0.5 & \frac{1}{12}\simeq 0.08 \\ \hline \end{array}
$$
IIReprésentations des données
1Effectifs et fréquences de valeurs
Nous reprenons les tableaux d'effectifs et de fréquences du I.2. :
$$ \begin{array}{|l|c|c|c|c|c|c|c|c|} \hline \text{Notes} & 2 & 6 & 7 & 9 & 10 & 11 & 14 & 16 \\ \hline \text{Effectifs} & 1 & 2 & 1 & 1 & 1 & 3 & 2 & 1 \\ \hline \text{Fréquences} & \frac{1}{12}\simeq 0.08 & \frac{1}{6}\simeq 0.17 & \frac{1}{12}\simeq 0.08 & \frac{1}{12}\simeq 0.08 & \frac{1}{12}\simeq 0.08 & \frac{1}{4}=0.25 & \frac{1}{6}\simeq 0.17 & \frac{1}{12}\simeq 0.08 \\ \hline \end{array}
$$
Les tableaux d'effectifs ou de fréquences peuvent être représentés par un diagramme en nuage de points obtenu en plaçant les points ayant pour abscisse les valeurs et en ordonnée les effectifs (ou fréquences) :

Nuage de points des effectifs |

Nuage de points des fréquences |
Les tableaux de fréquences peuvent être représentés en diagramme circulaire obtenu en coloriant pour chaque valeur un secteur angulaire de mesure égale à la fréquence multipliée par \(360°\) :
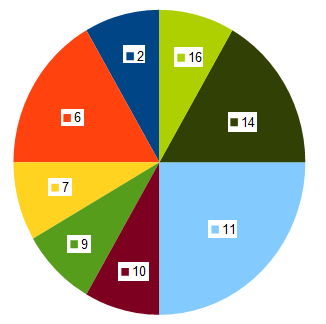

Diagramme circulaire
2Effectifs et fréquences de classes
Nous reprenons les tableaux d'effectifs et de fréquences du I.4. où les notes sont regroupées en 4 classes :
$$ \begin{array}{|l|c|c|c|c|} \hline \text{Notes} & [0;5[ & [5;10[ & [10;15[ & [15;20[ \\ \hline \text{Effectifs} & 1 & 4 & 6 & 1 \\ \hline \text{Fréquences} & \frac{1}{12}\simeq 0.08 & \frac{4}{12}\simeq 0.33 & \frac{6}{12}=0.5 & \frac{1}{12}\simeq 0.08 \\ \hline \end{array}
$$
Lorsque les données sont organisées en classes de mêmes amplitudes, il est possible de les représenter à l'aide d'histogramme. Chaque classe est représentée par un rectangle de largeur (en abscisse) valant l'amplitude (ici 5) et de hauteur (en ordonnée) valant l'effectif (ou la fréquence) :

Histogramme des classes d'effectifs |

Histogramme des classes de fréquences |